算法设计与分析实验：滑动窗口与二分查找

一、寻找两个正序数组的中位数

1.1 具体思路

1.2 流程展示

1.3 代码实现

1.4 代码复杂度分析

1.5 运行结果

二、X的平方根

2.1 具体思路

2.2 流程展示

2.3 代码实现

2.4 代码复杂度分析

2.5 运行结果

三、两数之和 II-输入有序数组

3.1 采用二分查找的思想

3.2 采用滑动窗口的思想

四、二叉搜索树中的插入操作

4.1 采用递归的思想

4.2 采用迭代的思想

一、寻找两个正序数组的中位数

力扣第四题

1.1 具体思路

本题采用二分查找的思想。

（1）按照题目中的条件，首先确保 nums1 中的长度小于等于 nums2 中的长度。如果不是这样，则交换数组以确保这个条件。

（2）初始化两个指针，在 nums1 中的切分位置 left 从 0 开始、right 从 nums1 的长度开始。在 nums1 中选取一个中间的位置进行切分，即 partition1 = (left + right) // 2。同时，根据 partition1 在 nums2 中对应的切分位置，即 partition2 = (m + n + 1) // 2 - partition1。

（3）创造四个变量：max_left1、min_right1、max_left2 和 min_right2。这些变量分别表示 partition1 左边部分的最大值、partition1 右边部分的最小值、partition2 左边部分的最大值和 partition2 右边部分的最小值。有一点需要注意，当 partition1 或 partition2 等于 0 或 m 或 n 的时候，需要将对应的变量赋值为正负无穷来避免越界错误。

（4）进行比较得出结果。如果 max_left1 小于等于 min_right2 且 max_left2 小于等于 min_right1，则找到了合适的切分位置。此时，中位数为 (max(max_left1, max_left2) + min(min_right1, min_right2)) / 2。否则，需要调整切分位置的范围。

（5）不断地调整切分位置的范围，直到找到合适的切分位置来得到中位数。

1.2 流程展示

假设两个数组如下，根据二分思想对其进行初步划分

nums1: [1, 3, 8, 9] max_left1 = 3 min_right1 = 8

nums2: [2, 7, 10, 12, 15] max_left2 = 7 min_right2 = 10

<--- partition1 --->

nums1: 1 | 3 8 9

<--- partition2 --->

nums2: 2 7 | 10 12 15

在切分位置上，nums1 的左半部分为 [1]，右半部分为 [3, 8, 9]

在切分位置上，nums2 的左半部分为 [2, 7]，右半部分为 [10, 12, 15]

max_left1 = 1 min_right1 = 3

max_left2 = 7 min_right2 = 10

因为 max_left1 <= min_right2 且 max_left2 > min_right1，所以需要继续调整切分位置。

将切分位置向右移动一位：

<--- partition1 --->

nums1: 1 3 | 8 9

<--- partition2 --->

nums2: 2 7 | 10 12 15

在切分位置上，nums1 的左半部分为 [1, 3]，右半部分为 [8, 9]

在切分位置上，nums2 的左半部分为 [2, 7]，右半部分为 [10, 12, 15]

max_left1 = 3 min_right1 = 8

max_left2 = 7 min_right2 = 10

因为 max_left1 <= min_right2 且 max_left2 <= min_right1，所以找到了合适的切分位置。

中位数：(max(max_left1, max_left2) + min(min_right1, min_right2)) / 2 = (8 + 8) / 2 = 8

1.3 代码实现

from typing import List

class Solution:
    def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
        # 确保 nums1 的长度小于等于 nums2 的长度
        if len(nums1) > len(nums2):
            nums1, nums2 = nums2, nums1

        m, n = len(nums1), len(nums2)
        left, right = 0, m
        median1, median2 = 0, 0

        while left <= right:
            # 在 nums1 的切分位置
            partition1 = (left + right) // 2
            # 在 nums2 中的相应切分位置
            partition2 = (m + n + 1) // 2 - partition1

            # 处理边界情况
            max_left1 = float('-inf') if partition1 == 0 else nums1[partition1 - 1]
            min_right1 = float('inf') if partition1 == m else nums1[partition1]
            max_left2 = float('-inf') if partition2 == 0 else nums2[partition2 - 1]
            min_right2 = float('inf') if partition2 == n else nums2[partition2]

            # 根据切分位置进行比较得出结果
            if max_left1 <= min_right2 and max_left2 <= min_right1:
                median1 = max(max_left1, max_left2)
                median2 = min(min_right1, min_right2)
                break
            elif max_left1 > min_right2:
                right = partition1 - 1
            else:
                left = partition1 + 1

        # 根据数组的总长度是奇数还是偶数来返回中位数
        if (m + n) % 2 == 0:
            return (median1 + median2) / 2
        else:
            return median1

nums1 = [1, 3]
nums2 = [2]
solution = Solution()
result = solution.findMedianSortedArrays(nums1, nums2)
print(f"{result:.5f}")  # 输出：2.00000

nums1 = [1, 2]
nums2 = [3, 4]
solution = Solution()
result = solution.findMedianSortedArrays(nums1, nums2)
print(f"{result:.5f}")  # 输出：2.50000

1.4 代码复杂度分析

这个算法的时间复杂度为O(log(min(m, n)))，其中m和n分别是nums1和nums2的长度。

算法的核心是使用二分查找来找到一个合适的切分位置，使得切分后的两个部分满足以下条件：

nums1和nums2被切分成左右两部分，分别为nums1_left和nums1_right、nums2_left和nums2_right。

左半部分的元素都小于或等于右半部分的元素。

在每一轮二分查找中，根据切分位置，在nums1和nums2中找到对应的切分点，然后比较切分点的左右元素，根据比较结果调整切分位置的范围。

最坏情况下，算法会进行O(log(min(m, n)))轮二分查找，每一轮查找的时间复杂度为O(1)，因此总的时间复杂度为O(log(min(m, n)))。

空间复杂度为O(1)，因为算法只使用了有限的额外变量来存储中间结果。没有使用额外的数据结构。

总结起来，该算法的时间复杂度为O(log(min(m, n)))，空间复杂度为O(1)。

1.5 运行结果

示例一：nums1 = [1, 3] nums2 = [2]

示例二：nums1 = [1, 2] nums2 = [3, 4]

结果如下

输出与预期一致

二、X的平方根

力扣第69题

2.1 具体思路

本题运用二分查找的思想。

首先，算术平方根的范围一定是在 [0, x] 的范围内，因此我们可以对这个范围进行二分查找。

我们用 left 和 right 分别表示左右边界，mid 表示中间位置。将 left 初始化为 0，right 初始化为 x。

每次循环时，让 mid 等于 left 和 right 的平均值。如果 mid 的平方等于 x，则 mid 就是 x 的算术平方根，直接返回 mid。

如果 mid 的平方小于 x，则说明要继续向右搜索算术平方根，在右半部分进行二分查找，因此将 left 更新为 mid+1。

如果 mid 的平方大于 x，则说明要往左边搜索算术平方根，在左半部分进行二分查找，因此将 right 更新为 mid-1。

上述过程重复执行，直到 left > right 为止。此时，left-1 就是 x 的算术平方根的值。

2.2 流程展示

left right

↓ ↓

----- ... ------[mid]------ ... ------[x]

mid^2 < x mid^2 > x

(left 更新为 mid+1) (right 更新为 mid-1)

初始时，left 的值为 0，right 的值为 x。

在每次循环中，我们计算 mid 的值，并比较 mid 的平方与 x 的大小关系。并执行如上更新。

这样不断循环直到 left > right 为止，最后返回 left-1，即为 x 的算术平方根的整数部分。

2.3 代码实现

def mySqrt(x: int) -> int:
    left, right = 0, x
    while left <= right:
        mid = (left + right) // 2
        if mid * mid == x:
            return mid
        elif mid * mid < x:
            left = mid + 1
        else:
            right = mid - 1
    return left - 1

# 示例测试代码
print(mySqrt(4))  # 输出：2
print(mySqrt(8))  # 输出：2
print(mySqrt(16))  # 输出：4

2.4 代码复杂度分析

时间复杂度：

while 循环中，每次二分法排除了一半的区间，因此时间复杂度为 O(logn)。

空间复杂度：

只定义了常数个变量，因此空间复杂度为 O(1)。

因此，整体时间复杂度为 O(logn)，空间复杂度为 O(1)。

2.5 运行结果

示例有4、8、10

由于返回类型为整数，因此预期的返回结果为2，2，3

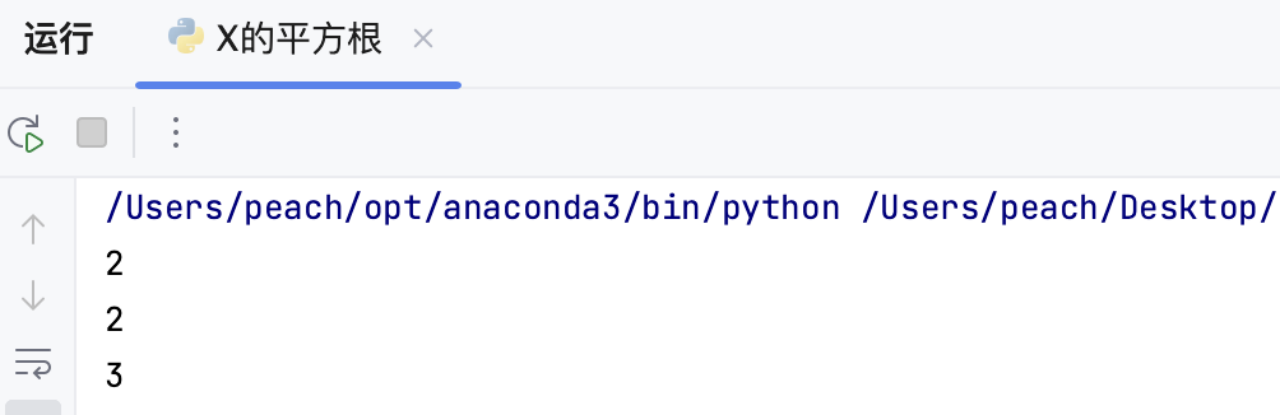
输出与预期结果一致

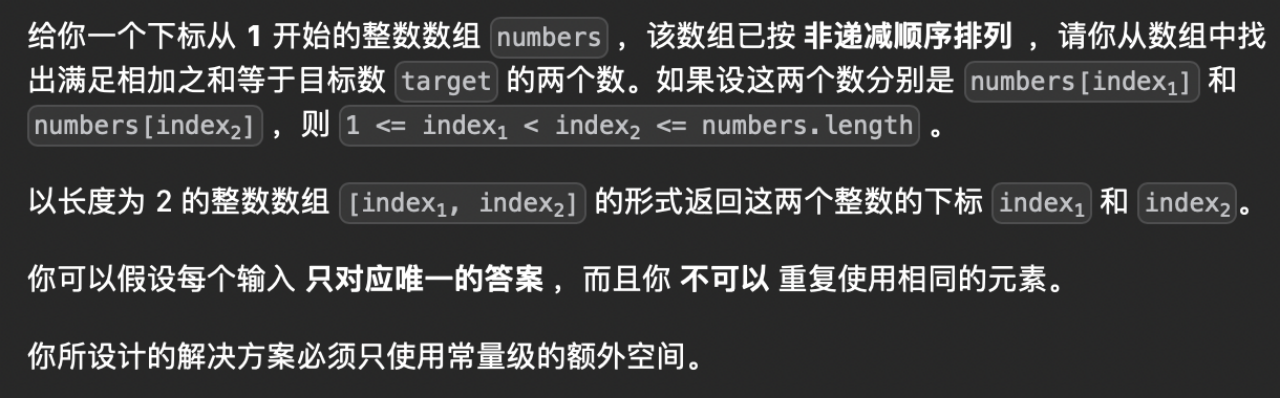
三、两数之和 II-输入有序数组

力扣第167题

3.1 采用二分查找的思想

（1）具体思路

若使用二分查找的思路，我们可以遍历数组中的每个元素，然后针对当前元素，在剩余部分中使用二分查找来寻找与之匹配的目标数。具体步骤如下：

遍历数组中的每个元素 numbers[i]。

在 numbers[i+1:] 的范围内使用二分查找，查找目标数 target - numbers[i]。

如果找到目标数，则返回 [i+1, j+1]，其中 j 是目标数在数组中的下标。

如果未找到目标数，则继续遍历下一个元素。若最后仍未找到，则返回[-1,-1]表示未找到。

对于二分查找，我们定义了一个 binary_search 函数，用于实现二分查找。它接收一个有序的整数数组 numbers，目标值 target，以及搜索范围的起始和结束下标 start 和 end。在 binary_search 函数中，我们通过不断更新起始和结束下标来缩小搜索范围，直到找到目标值或者确定目标值不存在。

（2）代码实现

from typing import List


def binary_search(numbers: List[int], target: int, start: int, end: int) -> int:
    while start <= end:
        mid = (start + end) // 2
        if numbers[mid] == target:
            return mid
        elif numbers[mid] < target:
            start = mid + 1
        else:
            end = mid - 1
    return -1


def twoSum(numbers: List[int], target: int) -> List[int]:
    n = len(numbers)
    for i in range(n):
        remaining = target - numbers[i]
        # 在 numbers[i+1:] 中使用二分查找
        j = binary_search(numbers, remaining, i + 1, n - 1)
        if j != -1:
            return [i + 1, j + 1]
    return [-1, -1]


# 示例测试代码
print(twoSum([2, 7, 11, 15], 9))  # 输出：[1, 2]
print(twoSum([2, 3, 4], 6))  # 输出：[1, 3]
print(twoSum([-1, 0], -1))  # 输出：[1, 2]

（3）复杂度分析

这段代码使用了二分查找来实现 twoSum 函数，下面是对其复杂度进行分析：

twoSum 函数中的循环遍历数组，时间复杂度为 O(n)，其中 n 是数组的长度。

在每次循环中，调用了 binary_search 函数进行二分查找。二分查找的时间复杂度为 O(logn)。

综上所述，整个算法的时间复杂度为 O(nlogn)。

空间复杂度方面，除了存储结果的列表外，算法没有使用额外的空间，因此空间复杂度为 O(1)。

需要注意的是，输入的数组在调用 twoSum 函数之前没有要求是有序的。如果输入的数组是有序的，则可以使用双指针的方法来进一步优化时间复杂度为 O(n)，即我们采用的第二种思想-滑动窗口。

3.2 采用滑动窗口的思想

（1）具体思路

算法思路如下：

定义两个指针 left 和 right，分别指向数组的最左端和最右端。

循环进行以下操作，直到找到满足条件的两个数或者 left >= right：

计算当前窗口的和 currSum = numbers[left] + numbers[right]。

如果 currSum 等于目标数 target，则返回结果 [left + 1, right + 1]。

如果 currSum 大于目标数 target，说明当前窗口的和太大了，需要将窗口右侧向左移动，即 right -= 1。

如果 currSum 小于目标数 target，说明当前窗口的和太小了，需要将窗口左侧向右移动，即 left += 1。

如果循环结束都没有找到满足条件的两个数，则返回 [-1, -1]。

（2）流程展示

假设目标数为9，数组为[2, 4, 6, 8, 10, 12]。

初始情况下，左右指针分别指向数组的最左端和最右端，构成一个长度为数组长度的窗口。窗口内的数之和为14，大于目标数9。

接着，我们将右指针左移一格：

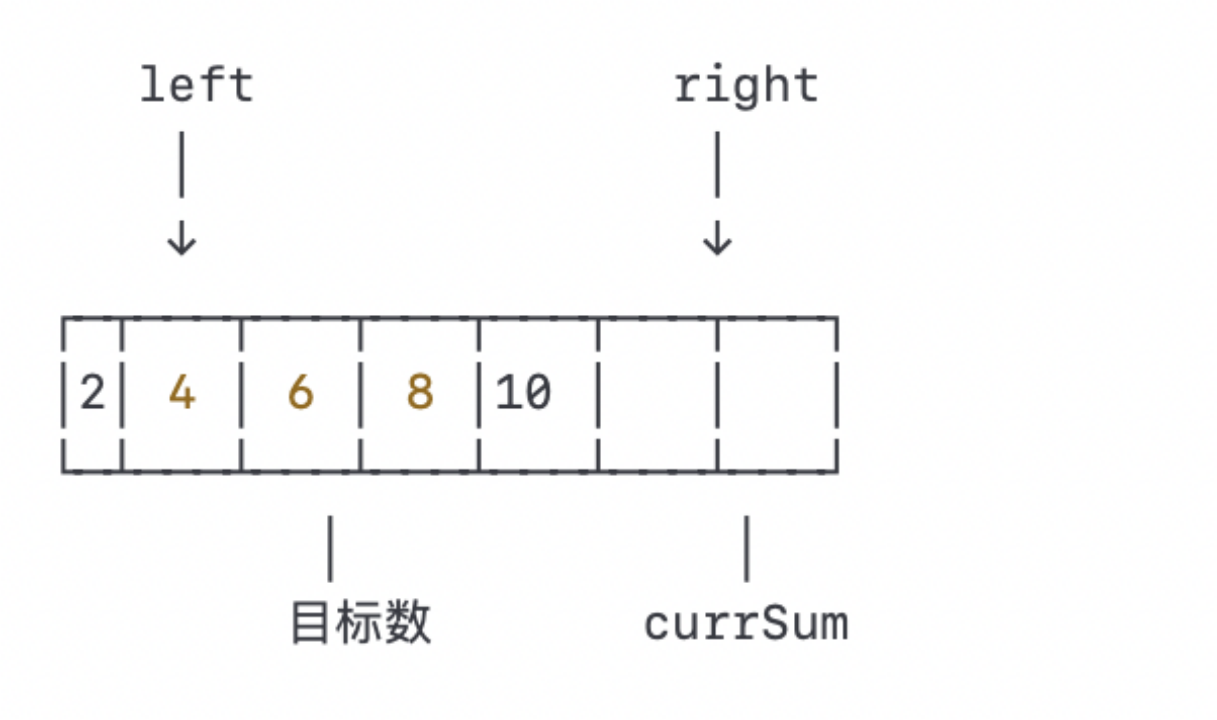
当前窗口的数之和为12，仍然大于目标数9。我们再次将右指针左移一格：

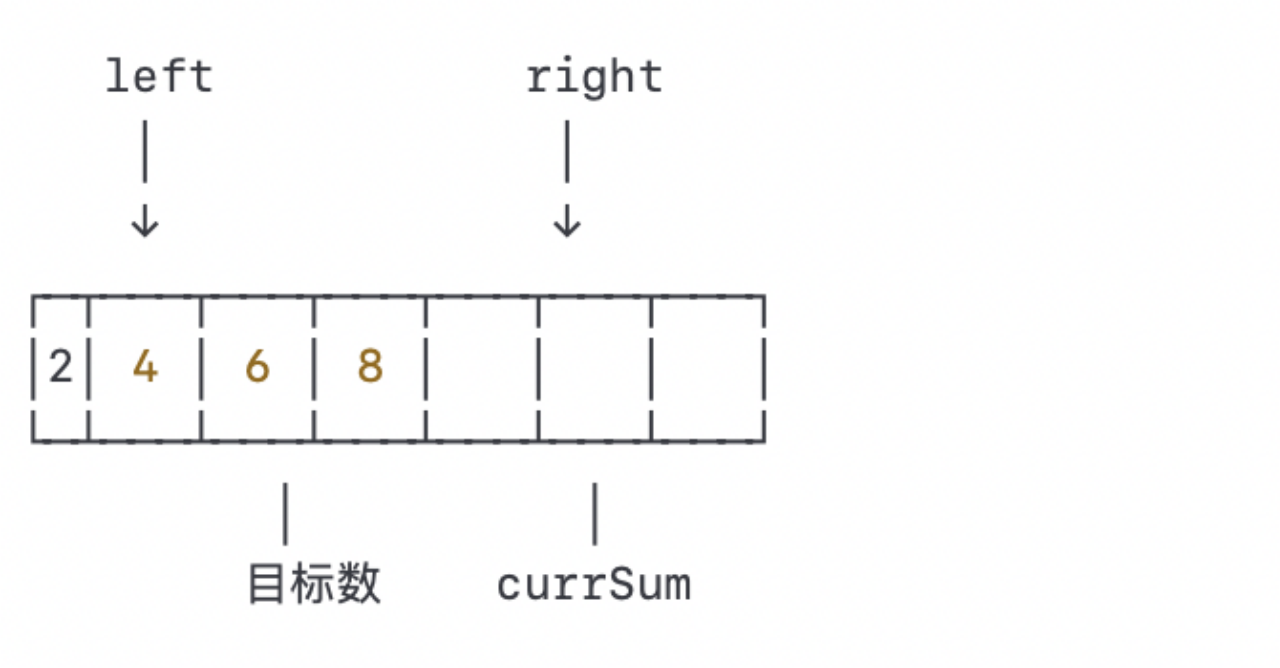
当前窗口的数之和为10，仍然大于目标数9。我们再次将右指针左移一格：

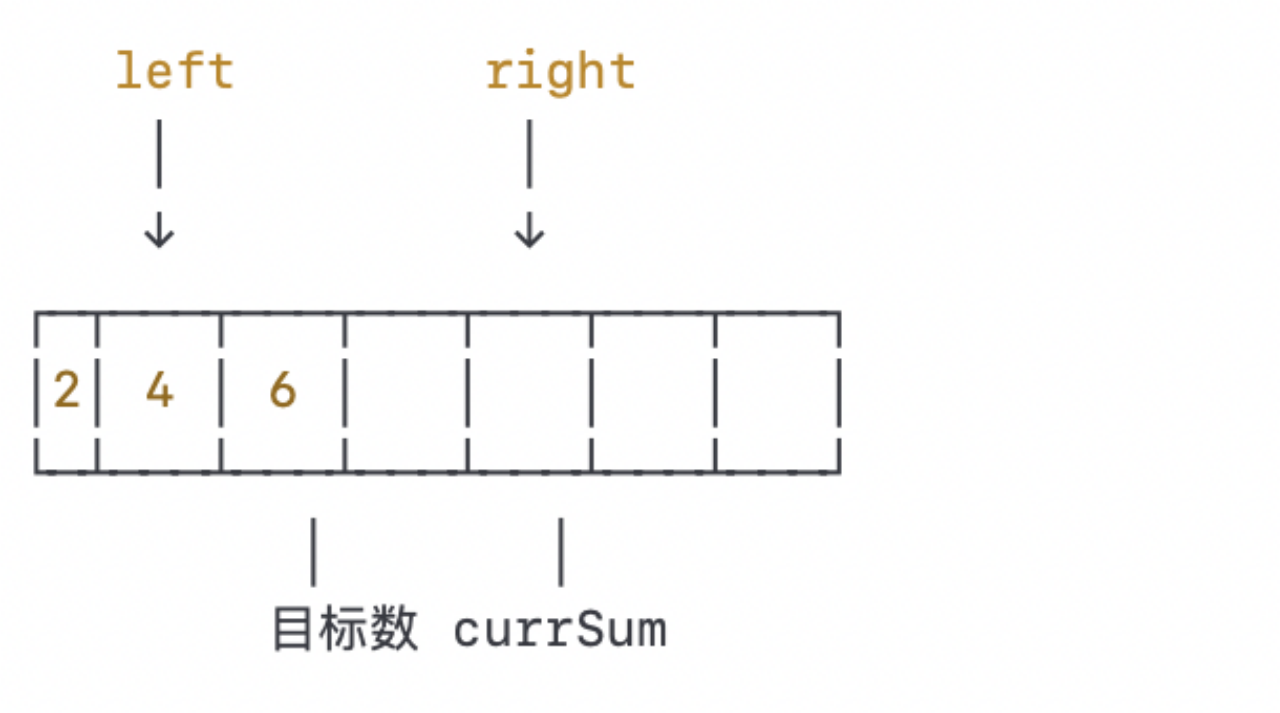
当前窗口的数之和为6，小于目标数9。我们将左指针右移一格：

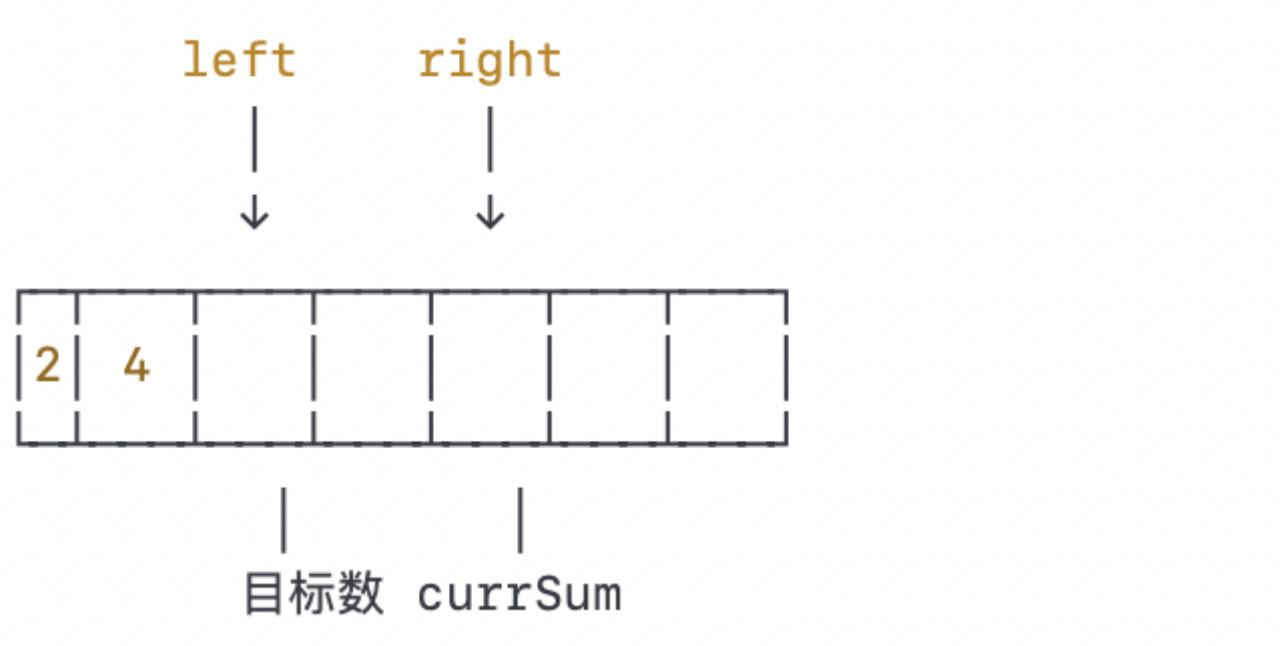
当前窗口的数之和为6，仍然小于目标数9。我们再次将左指针右移一格：

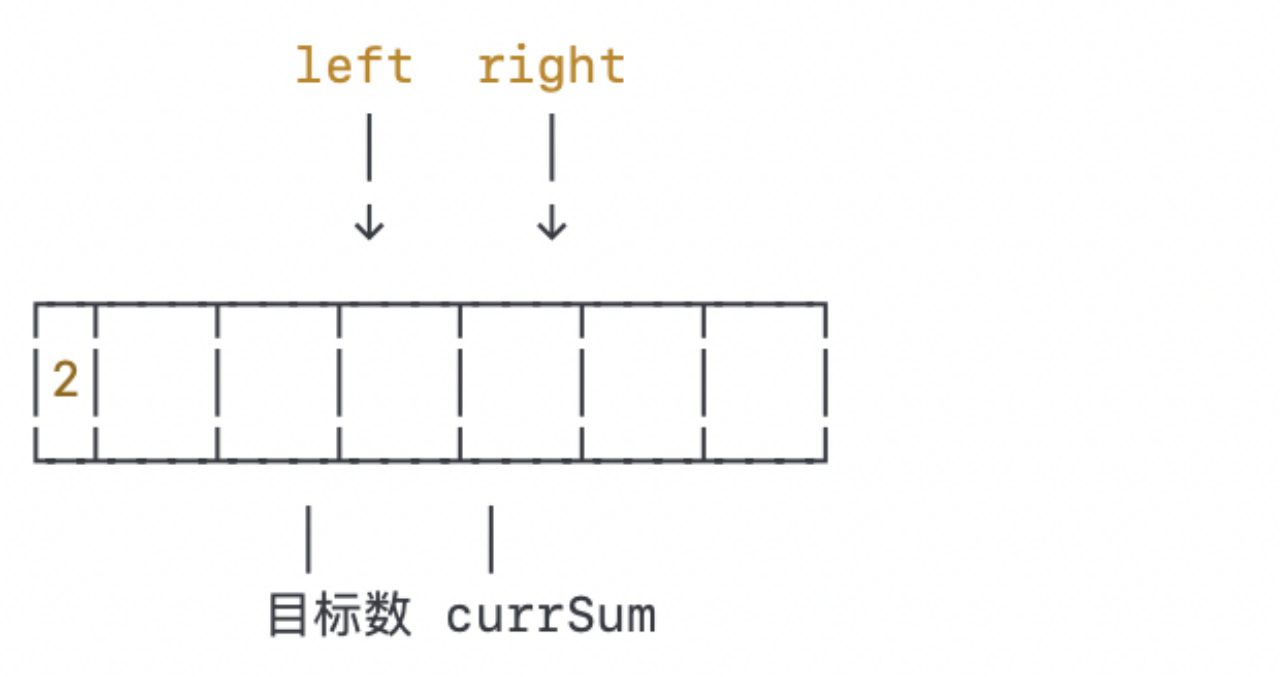
当前窗口的数之和为2，仍然小于目标数9。我们再次将左指针右移一格：

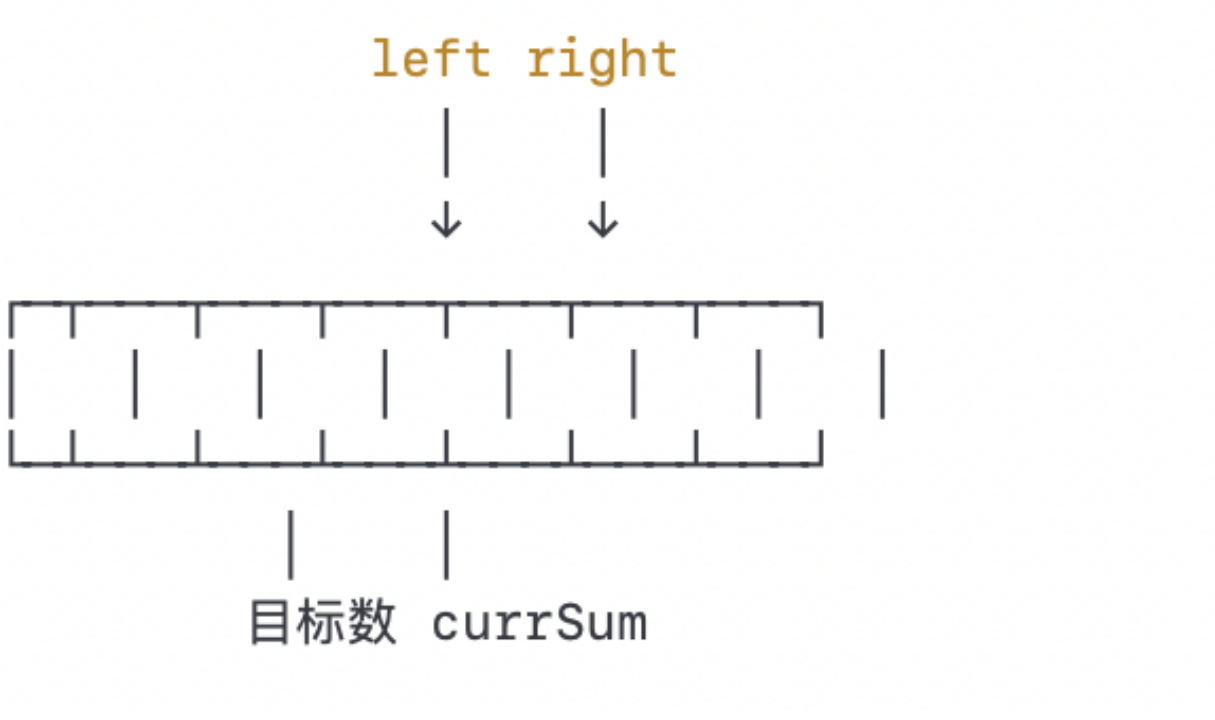
当前窗口的数之和为0，仍然小于目标数9。此时，左右指针已经相遇，并且没有找到符合要求的两个数。因此返回 [-1, -1] 表示未找到。

（3）代码实现

#滑动窗口
from typing import List

def twoSum(numbers: List[int], target: int) -> List[int]:
    left, right = 0, len(numbers) - 1
    while left < right:
        currSum = numbers[left] + numbers[right]
        if currSum == target:
            return [left + 1, right + 1]
        elif currSum > target:
            right -= 1
        else:
            left += 1
    return [-1, -1]


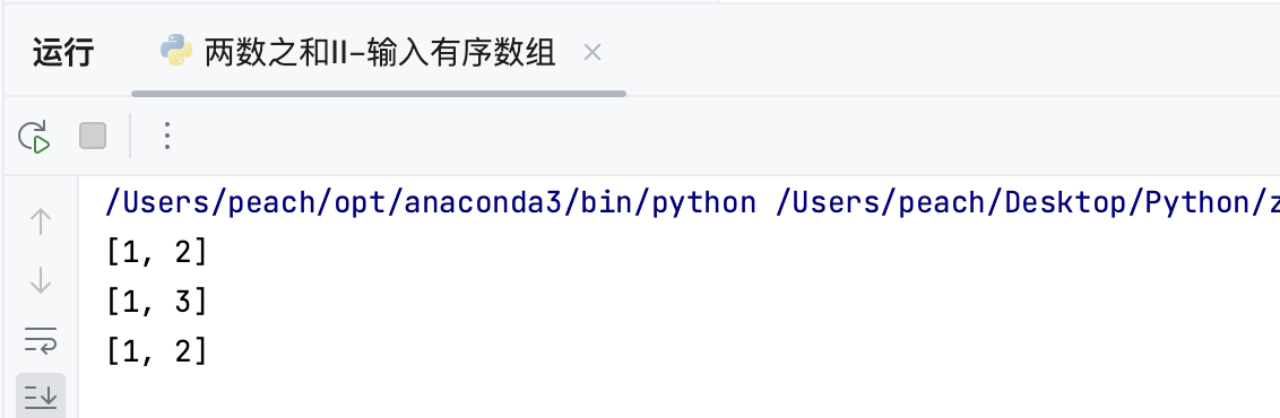
print(twoSum([2, 7, 11, 15], 9))  # 输出：[1, 2]
print(twoSum([2, 3, 4], 6))  # 输出：[1, 3]
print(twoSum([-1, 0], -1))  # 输出：[1, 2]

（4）代码复杂度分析

这个算法的时间复杂度是 O(n)，其中 n是数组的长度。因为左右指针移动的次数最多为 n次，每次移动指针需要 O(1) 的时间，所以总时间复杂度为 O(n)。

空间复杂度为 O(1)，因为没有使用额外的数据结构。

（5）运行结果

示例1:[2, 7, 11, 15], 9

示例2:[2, 3, 4], 6

示例3:[-1, 0], -1

运行结果均符合预计

四、二叉搜索树中的插入操作

力扣第702题

4.1 采用递归的思想

（1）具体思路

如果当前节点为空，则将新值插入到当前位置。

如果新值小于当前节点的值，则继续在当前节点的左子树中插入新值。

如果新值大于当前节点的值，则继续在当前节点的右子树中插入新值。

最后返回根节点。

（2）流程展示

初始树:

/ \

2 7

/ \

1 3

插入新值 5：

/ \

2 7

/ \ \

1 3 5

这个过程中，我们首先从根节点开始，比较新值 5 和当前节点值 4，由于 5 大于 4，所以我们移动到右子树继续比较。

在右子树中，新值 5 比当前节点值 7 小，所以我们将新值插入到右子树的左子树位置。

最终的结果是，树中正确地插入了新值 5。

（3）代码实现

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

def insertIntoBST(root: TreeNode, val: int) -> TreeNode:
    if not root:
        return TreeNode(val)
    if val < root.val:
        root.left = insertIntoBST(root.left, val)
    else:
        root.right = insertIntoBST(root.right, val)
    return root

def treeToList(root):
    result = []

    def inorderTraversal(node):
        if not node:
            return
        inorderTraversal(node.left)
        result.append(node.val)
        inorderTraversal(node.right)

    inorderTraversal(root)
    return result

# 创建示例树 [4,2,7,1,3]
root = TreeNode(4)
root.left = TreeNode(2)
root.right = TreeNode(7)
root.left.left = TreeNode(1)
root.left.right = TreeNode(3)

# 插入新值 5
new_val = 5
new_root = insertIntoBST(root, new_val)

# 将树转换为列表
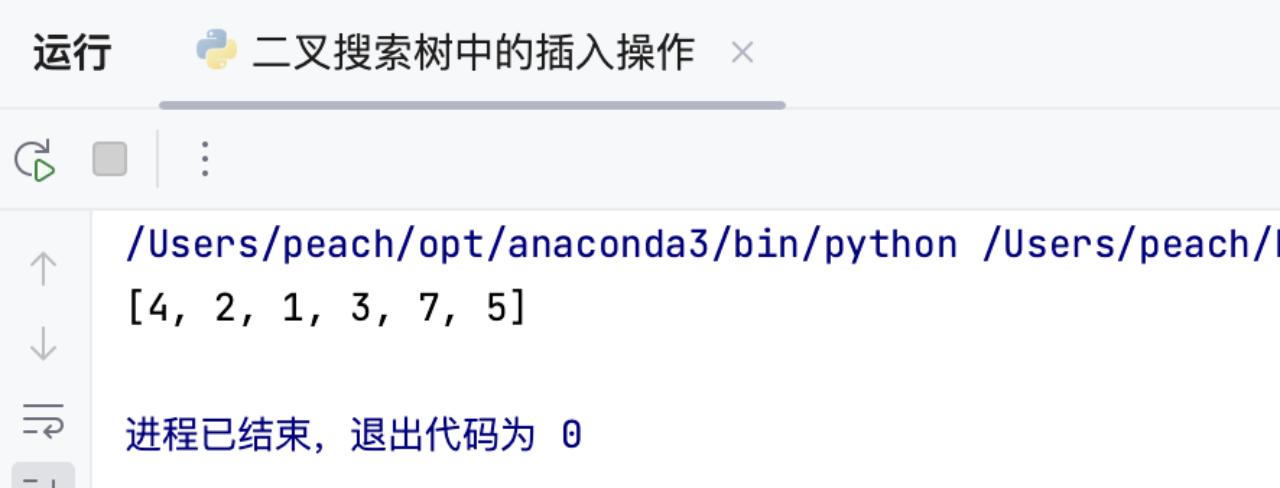
result_list = treeToList(new_root)
print(result_list)

（4）代码复杂度分析

对于插入操作的时间复杂度分析：

最好情况下，树是平衡的，每个节点的左右子树大小相差不大于 1。在这种情况下，插入节点的时间复杂度为 O(logN)，其中 N 是树中节点的数量。

最坏情况下，树是非平衡的，形成了一个链表结构。在这种情况下，插入节点的时间复杂度为 O(N)，其中 N 是树中节点的数量。

因此，在平均情况下，插入节点的时间复杂度为 O(logN)。

对于将二叉搜索树转换为列表的操作，需要进行中序遍历，即遍历所有节点。因此，时间复杂度是 O(N)，其中 N 是树中节点的数量。

综上所述，插入节点的时间复杂度为 O(logN)，将树转换为列表的时间复杂度为 O(N)。

空间复杂度方面，由于使用了递归操作，在递归过程中会使用额外的堆栈空间。递归的深度取决于树的高度，在最坏情况下为 O(N)，其中 N 是树中节点的数量。因此，空间复杂度为 O(N)，除了输入和输出所占用的空间。

4.2 采用迭代的思想

（1）具体思想

如果根节点为空，则直接创建一个新节点作为根节点，返回根节点。

如果插入的值小于当前节点的值，并且当前节点的左子树为空，则将新节点插入为当前节点的左子节点，返回根节点。

如果插入的值大于当前节点的值，并且当前节点的右子树为空，则将新节点插入为当前节点的右子节点，返回根节点。

如果插入的值小于当前节点的值，将当前节点移动到左子节点继续插入的位置。

如果插入的值大于当前节点的值，将当前节点移动到右子节点继续插入的位置。

重复上述步骤直到找到合适的插入位置。

（2）流程展示

首先，创建一个空的二叉搜索树：

(empty)

接下来，按照迭代思想插入节点的过程：

插入节点值为 4：

插入节点值为 2：

插入节点值为 7：

/ \

2 7

插入节点值为 1：

/ \

2 7

插入节点值为 3：

、 4

/ \

2 7

/ \

1 3

以上就是按照迭代思想依次插入节点到二叉搜索树中的过程，并得到了最终的二叉搜索树。

（3）代码实现

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

def insertIntoBST(root: TreeNode, val: int) -> TreeNode:
    if not root:
        return TreeNode(val)

    node = root
    while node:
        if val < node.val:
            if not node.left:
                node.left = TreeNode(val)
                break
            else:
                node = node.left
        else:
            if not node.right:
                node.right = TreeNode(val)
                break
            else:
                node = node.right

    return root

# 创建示例树 [4,2,7,1,3]
root = TreeNode(4)
root.left = TreeNode(2)
root.right = TreeNode(7)
root.left.left = TreeNode(1)
root.left.right = TreeNode(3)

# 插入新值 5
new_val = 5
new_root = insertIntoBST(root, new_val)

# 中序遍历树，将树转换为列表
def inorderTraversal(node):
    if not node:
        return []
    return inorderTraversal(node.left) + [node.val] + inorderTraversal(node.right)

result_list = inorderTraversal(new_root)
print(result_list)

（4）复杂度分析
对于插入一个新节点，上述算法的时间复杂度为 O(h)，其中 h 为树的高度。

由于二叉搜索树的高度与其中的节点数量相关，因此在最坏情况下（即插入的节点值是原来树中最大或最小的），时间复杂度为 O(n)，其中 n 表示树中节点的数量。

但是平衡二叉搜索树（如 AVL 树、红黑树）可以保证树的高度为 O(log n)，因此插入新节点的时间复杂度也可以控制在 O(log n) 级别。

对于空间复杂度，递归实现需要调用栈空间，而迭代实现只需要一个额外指针变量 node，因此空间复杂度都是 O(1)。

（5）运行结果

输入：root = [4,2,7,1,3], val = 5

输出：[4,2,7,1,3,5]

记得天天开心哦～～～